先日はてぶに 興味深いデータ構造:BK 木 | プログラミング | POSTD という翻訳記事 ( 元記事 http://signal-to-noise.xyz/post/bk-tree/) があがっているのをみて初めて BK-tree というものを知ったので,golang で実装してみました.
BK-tree とは
先程の記事に全部書いてあるのですが… BK-tree は,ある距離空間内で近傍点探索を効率的に行えるデータ構造です.利用例としてはスペルチェックや類似画像検索などがあります.
距離空間とは,なにかしらの距離を計算することができる空間のことで,距離としてハミング距離やマンハッタン距離,レーベンシュタイン距離,ユークリッド距離などなどが挙げられます. 例えば,いわゆる普通の 3 次元の空間は,ユークリッド距離を距離関数に持つ距離空間と考えられます.
近傍点探索は,要するにある点に対して,近くにある点を探すことです.
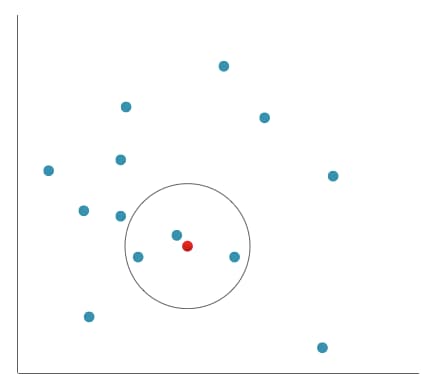
ものすごく単純に近傍点探索をやろうと思うと,全要素を線形に探索して距離を計算していく必要があります. そこで BK-tree を使うともっと計算量が減らせるというわけなのです.(ちなみに僕は BK-tree を使った場合の計算量がよくわかっていません.実験的に速いことを確認しただけです.正確な計算量は考えてもよくわかりませんでした…)
構造や仕組みは元記事などをご参照ください.
golang での bk-tree 実装は実はいくつかあったのですが,単純にアルゴリズムを理解するために実装したかったのと,レーベンシュタイン距離を距離関数として使うことを前提にしていたりとちょっと自分の用途に合っていない気がしたので,別で作ってみました.
このパッケージでは,スペルチェックそのものや距離関数を提供していません.BK-tree というデータ構造だけを提供しています.
使用例
16 bit 整数を要素,ハミング距離を距離関数とした例です.
要素となる型は bktree.Entry interface を満たす必要があります.これは Distance(Entry) int を要求する interface です.
本当は distance<T: Entry>(x: T) -> int みたいな形にしたいのですが,golang だと出来ないので,実装側で e.(hashValue) のように型アサーションする必要があります.
ここでは uint16 に戻してハミング距離を計算しています.
要素の追加は Add(e Entry) です.
ここでは 0 ~ 0xffff までを突っ込んでいます.
探索は Search(e Entry, tolerance int) []*Result です.
第一引数がキー,第二引数が許容する距離の最大値です.
package main
import (
"fmt"
"github.com/agatan/bktree"
)
type hashValue uint16
// Distance calculates hamming distance.
func (h hashValue) Distance(e bktree.Entry) int {
a := uint16(h)
b := uint16(e.(hashValue))
d := 0
var k uint16 = 1
for i := 0; i < 16; i++ {
if a&k != b&k {
d++
}
k <<= 1
}
return d
}
func main() {
var tree bktree.BKTree
// add 0x0000 to 0xffff to the tree.
for i := 0; i < 0xffff; i++ {
tree.Add(hashValue(i))
}
// search neighbors of 0x0000 whose distances are less than or equal to 1.
results := tree.Search(hashValue(0), 1)
for \_, result := range results {
fmt.Printf("%016b (distance: %d)\n", result.Entry.(hashValue), result.Distance)
}
}
これを実行すると,
0000000000000000 (distance: 0)
0000000000000001 (distance: 1)
0000000000000010 (distance: 1)
0000000000000100 (distance: 1)
0000000000001000 (distance: 1)
0000000000010000 (distance: 1)
0000000000100000 (distance: 1)
0000000001000000 (distance: 1)
0000000010000000 (distance: 1)
0000000100000000 (distance: 1)
0000001000000000 (distance: 1)
0000010000000000 (distance: 1)
0000100000000000 (distance: 1)
0001000000000000 (distance: 1)
0010000000000000 (distance: 1)
0100000000000000 (distance: 1)
1000000000000000 (distance: 1)という感じで 0x0000 とのハミング距離が 0 ~ 1 である要素がとれます.
パフォーマンス
単純な線形探索との比較をするベンチマークをおいてあります.
64 bit 整数,距離関数はハミング距離,データ量 1,000,000 件での結果が以下のようになりました.
| ベンチマーク | 実行時間 |
|---|---|
| BK-tree (完全一致) | 1108 ns/op |
| BK-tree (fuzziness 1) | 29468 ns/op |
| BK-tree (fuzziness 2) | 328753 ns/op |
| BK-tree (fuzziness 4) | 5490888 ns/op |
| BK-tree (fuzziness 8) | 68182122 ns/op |
| BK-tree (fuzziness 32) | 353715305 ns/op |
| Linear Search | 4132926 ns/op |
fuzziness が小さければ小さいほど ( = tolerance が小さければ小さいほど ) 高速に探索できることが分かります.
また,データ量が増えるほど Linear Search より有利になるので,距離に対してデータが十分に大量にある場合はかなり有効といえそうです.
おまけ
tree の構築にかかるコストがそこそこ大きかったので pprof で見つつチューニングする必要がありました. 学びとして,「map が重い」「interface が重い」というのがありました.
各ノードの部分木は,そのノードからの距離 d を key として,map[int]*Node としていました.
tree を構築する際には,allocate + read + write をかなりの回数行うのですが,これがまぁ遅い.
最終的にこの部分はスライスでもっておいて,d を key として部分木をとりたい時は線形探索をするようにしました.
next, ok := n.children[d] としていた部分が
type elem struct
distance int
node *node
}
for \_, c := range n.children {
if c.distance == d {
return c.node
}
}
return nil
という感じになります.あんまりきれいではないんですが,こっちの方がほとんどのケース倍以上速かったので,こちらを採用しました.
部分木の数が増えてくると,map のほうが速いと思われるのですが,ハミング距離の場合最大でも bit 数までしか部分木が増えないので.
レーベンシュタイン距離を用いたスペルチェックの場合でも,単語の最大文字数以上の距離にはなりません. 2 次元 / 3 次元程度の距離空間なら kd-tree などもっと他に良い方法があるきがするので,レーベンシュタイン距離やハミング距離を使うケースをメインに考えました.
その結果,実行時間のかなりの割合が Entry interface を介した関数呼び出しのオーバヘッドとか,inteface の allocation になってしまいました.
データ構造を golang で提供する以上このオーバヘッドは避けられないです.( もちろん BK-tree そのものを,自分の利用形態に特化して作れば回避できますが… )
ちょっと Rust や C++ で書きたくなりました.十分速いし書きやすいので良いんですが…